تعامد (هندسة)

في الهندسة الرياضية، يعتبر خطان أو مستويان (أو خط ومستوى) متعامدين (بالإنجليزية: perpendicular)‏ على بعضهما إذا شكلا زوايا متجاورة متطابقة (على شكل حرف T). ففي الشكل 1، القطعة المستقيمة AB متعامدة على القطعة المستقيمة CD في النقطة B، ويعبر عن تعامد المستقيمين AB وCD بعبارة: $AB\perp CD$ .

شكل 1: الخط AB عمودي على الخط CD، لأن كلا الزاويتين التان يشكلهما (اللونين البرتقالي والأزرق) تساوي 90 درجة

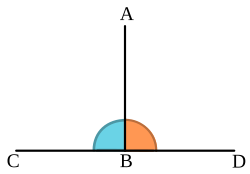
جميع الزوايا المكونة من تعامد خطين مستقيمين هي زوايا قائمة (قياس الزاوية القائمة يساوي ½ π راديان، أو 90° درجة). وبالعكس فإن أي خطين مستقيمين يشكلان زوايا قائمة فهما متعامدان .

المعايير الرياضية

في النظام الإحداثي الديكارتي يمكن وصف خطين مستقيمين ل1 ول2 بالمعادلتين التاليتين:

ل1: y = a×x + b

ل2: y = c×x + d

طالما أن كلاً من الخطين المستقيمين غير رأسي، فإن ميل ل1 هو a وميل ل2 هو c. ويكون الخطان المستقيمان ل1 ول2 متعامدين إذا كان حاصل ضرب ميليهما يساوي -1، أي a × c = -1 .

وفي الهندسة التحليلية، يكون المتجهان متعامدين إذا كان: ميل الأول × ميل الثاني = -1

إنشاء العمودي

شكل 2: طريقة إسقاط عمودي (الأزرق) على المستقيم AB من النقطة P

إنشاء عمودي على مستقيم من نقطة خارجه

لإسقاط عمودي على المستقيم AB يمر بالنقطة P باستخدام الفرجار والمسطرة نقوم بالخطوات التالية (انظر شكل 2):

• (الأحمر): ارسم دائرة مركزها النقطة P لتقطع الخط المستقيم AB في A' وB'، فتكونان متساويتا البعد عن P,
• (الأخضر): ارسم دائرتين مركزهما النقطتان A' وB' وتمران بالنقطة P. نفترض أن النقطة الأخرى لتقاطعهما هي Q
• (الأزرق): صل النقطتين P وQ لتحصل على العمودي المطلوب PQ

شكل 3: إنشاء عمودي على مستقيم من نقطة عليه (B) - خطوة 1

إنشاء عمودي على مستقيم من نقطة عليه

لإنشاء عمودي على خط مستقيم من نقطة عليه نقوم بالخطوات التالية

• ارسم دائرة مركزها هذه النقطة (B مثلاً) وتقطع الخط المستقيم في نقطتين A و A' (انظر شكل 3)
• من النقطتين A و A' نرسم دائرتين لهما نفس نصف القطر ونصف قطرهما أكبر من المسافة AB
• نصل نقطتي تقاطع هاتين الدائرتين لنحصل على العمودي المطلوب

شكل 4: طريقة رسم قاطع عمودي على خط مستقيم

إنشاء عمودي على مستقيم في أي موضع منه

لإنشاء عمودي على خط مستقيم في أي موضع منه نقوم بالخطوات التالية (انظر شكل 4):

• (الأزرق): من أي نقطتين على الخط المستقيم نرسم دائرتين متقاطعتين
• (الأحمر): نصل بين نقطتي تقاطع الدائرتين فنحصل على العمودي المطلوب

شكل 5: الخطان a و b متوازيان ويقطعهما القاطع c

بالنسبة للخطوط المتوازية

المقالة الرئيسة: مسلمة التوازي

كما هو موضح في شكل 5، إذا كان كل من خطين مستقيمين (a و b) متعامدا على خط ثالث (c)، فإن كل الزوايا الناتجة عن التقاطع مع هذا الخط الثالث تكون زوايا قائمة. وبناء على ذلك، فإنه في الهندسة الإقليدية، أي خطين مستقيمين كل منهما عمودي على خط ثالث فهما متوازيان، بناءً على مسلمة التوازي. وبالعكس، فإن أي خط مستقيم عمودي على خطً مستقيمٍ ثانٍ، فإنه يكون عمودياً على أي خط مستقيم موازٍ له.

في شكل 5، كل الزوايا المظللة بالبرتقالي هي زوايا متطابقة، لأن الزوايا المتقابلة بالرأس متطابقة وكذلك الزوايا الداخلية المتبادلة الناشئة عن قاطع لخطين متوازيين هي متطابقة. ومن ثم، فإنه إذا كان خطان a و b متوازيين فإن أياً من النتائج التالية تؤدي للنتائج الأخرى كلها:

• إحدى زوايا الشكل هي زاوية قائمة
• إحدى الزوايا المظللة باللون البرتقالي مطابقة لإحدى الزوايا المظللة باللون الأخضر
• الخط المستقيم c عمودي على الخط المستقيم a
• الخط المستقيم c عمودي على الخط المستقيم b

إيجاد المتعامدات على دالة

في الجبر

في الجبر، لأي معادلة خطية (y = m × x + b)، فإن ميل المتعامدات عليها هو (-1/m)، المعكوس الجمعي لمقلوب ميل المعادلة الأصلية.

ولإيجاد العمودي على خط مستقيم (y = m × x + b) ويمر أيضاً بالنقطة (x، y) نحل المعادلة y = (-1/m) × x + b، بتعويض قيم m وَ x وَ y المعلومة لإيجاد قيمة b في معادلة الخط المطلوب.

في التفاضل

في التفاضل، لإيجاد العمودي على دالة نحسب مشتقة هذه الدالة، فيكون هذا هو ميله (m) عند أي نقطة (x، y). فنقوم بحل المعادلة y = (-1/m) × x + b، بتعويض قيم m وَ x وَ y المعلومة لإيجاد قيمة b في معادلة الخط المطلوب.

رمز التعامد

رمز التعامد هو $\perp$. فمثلاً $AB\perp CD$ تعني أن الخط المستقيم AB عمودي على الخط المستقيم CD، وتقرأ: AB عمودي على CD. الكود الخاص بهذا الرمز في مجموعة حروف يونيكود هو U+27C2 وهو ضمن الرموز الرياضية المتنوعة-المجموعة أ (بالإنجليزية: Miscellaneous Mathematical Symbols-A range)‏، وهو شبيه برمز التاك المقلوبة (U+22A5) لكنه حرف مختلف.

التعامد بين مستويين (هندسة وصفية)

يكون مستوى بيتا عمودي (اللون الابيض) على آخر الفا (اللون الاخضر) إذا كان لدى بيتا خط عمودي على الفا. علما بأن خط يكون عمودي على مستوى إذا كان الإسقاطات العمودية للخط عمودية على اثار المستوى.

في المثال المرفق معلومة الاسقاطات العمودية لخط ر (اللون الازرق) ومستوى الفا (اللون الاخضر)، مطلوب تحديد المستوى الذي يمر بالخط ر بحيث يكون عمودي على الفا. ومن ثم التحقق من النتيجة النهائية عن طريق عملية الدوران على مستوى الاسقاط الأول كما هو مبين في الجهة اليمنى من الصورة المرفق.

تعامد بين مستويين

التعامد بين خط ومستوى

يكون الخط r عموديًا على مستوى الفا إذا كان عمودي على جميع خطوط الفا التي تمر بنقطة التقاء r مع الفا وبما أنه لا يمكننا التحقق من جميع الخطوط التي تمر عبر نقطة الالتقاء بين الخط والمستوى ، فيكفي ان يكون الخط r عمودي على الأقل على خطين من الفا.

للتفصيل، يكون خط r عمودي على مستوى ألفا (α) إذا كان عمودي على خطين، m و n ، ينتميان للمستوى α. وبعد ذلك ، أي خط يتم الحصول عليه كتقاطع بين α وأي مستوى يمر بالخط r ، يكون عمودي على r.

يمكن الحصول بسهولة على الخطين المذكورين أعلاه m و n باستخدام مستويين بيتا (β) وجاما (γ) عموديين على α وعلى مستويات الإسقاط π1 و π2 - يكون المستوى β رأسي ويقطع α وفقًا للخط m. ويسمى خط أقصى انحدار α بالنسبة لمستوى الإسقاط الأول π1 - ويكون المستوى γ عمودي على مستوى الإسقاط الثاني π2 ويقطع ألفا وفقًا لـلخط n. الذي يمكن تعريفها كخط أقصى ميل ألفا بالنسبة ل π2.

وباختصار يتم الحصول على الخطين m و n في هذه الحالة كتقاطع بين α ومستويين α و γ ، اللذين يمران بالخط r ويكونان عموديين على α وعلى مستويات الإسقاط π1 و π2.

يكون خط عمودي على مستوى عندما يكون عمودي على خطين من المستوى

معرض صور

• 
  لماذا في الاسقاطات العمودية نرسم اسقاطات الخط r عمودية على اثار المستوى الفا ؟

انظر أيضاً

• إنشاءات الفرجار والمسطرة
• توازي (هندسة)
• زاوية قائمة
• منصف
• ناظم السطح

وصلات خارجية

• "إنشاء عمودي على شعاع من بدايته". Math open Reference (مرجع الرياضيات المفتوح) (بالإنجليزية). Archived from the original on 2019-06-10. Retrieved 2011-11-21. {{استشهاد ويب}}: روابط خارجية في |عمل= (help)صيانة الاستشهاد: لغة غير مدعومة (link)