تقنية رحلة أويلر

لا توجد نسخ مراجعة من هذه الصفحة، لذا، قد لا يكون التزامها بالمعايير متحققًا منه.

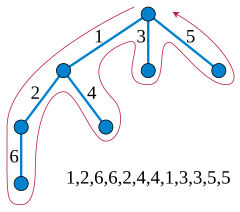
تقنية رحلة أويلر

تقنية رحلة أويلر(Euler tour technique (ETT)),سميت على اسم ليونهارت أويلر Leonhard Euler,هي عملية في نظرية البيان (graph theory) لتمثيل الأشجار. الشجرة ممثلة كبيان موجه (directed graph) يحتوي وصلتين موجهتين (directed edge) لكل وصلة في الشجرة, بعد ذلك يمكن للشجرة أن تمثل كحلقة أويلرية (Eulerian circuit ) من البيان الموجه, تقنية أويلر تسمح بحساب نظير (parallel computation) فعال لحلول مسائل شائعة في نظرية البيان الخوارزمي (algorithmic graph theory). تم تقديمها لأول مرة من قبل تارجان وفيشكن في 1984(Tarjan and Vishkin).

الإنشاء:

معطى شجرة غير موجهة ممثلة بمجموعة وصلات, تمثيل تقنية رحلة أويلر يمكن بناؤه بالتوازي كما يلي:

ننشئ لائحة متناسقة من الوصلات الموجهة:
لكل وصلة غير موجهة {u,v} في الشجرة, أدرج (u,v) و (v,u) في لائحة الوصلات.
رتب لائحة الوصلات معجميا (lexicographically)( نفترض هنا أن عقد(nodes) الشجرة مرتبة,و أن الجذر (root) هو أول عنصر في هذا الترتيب).
أنشئ لائحة المجاورة (adjacency list) لكل عقدة (مسماة next) وخريطة من العقد إلى أول الداخلين الى لائحة المجاورة(مسماه first).
لكل وصلة (u,v) في اللائحة و قم بالتوازي:
اذا كانت الوصلة السابقة (x,y) بحيث x ≠ u, اذن ابدأ من عقدة مختلفة, و عين first(u)=(u,v).
غير ذلك إذا كانت x = u, ابدأ من نفس العقدة, عين next(x,y)=(u,v).
أنشئ لائحة وصلات (مسماه succ) في ترتيب أويلر تور عبر تعيين مؤشرات succ(u,v) لكل الوصلات (u,v) بالتوازي متبعا القاعدة التالية:
اللائحة الناتجة succ ستكون حلقية.
البناء الكلي يأخذ عمل W(n) = (O(sort(n)).
الوقت المأخوذ حتى يتم ترتيب n عنصر بالتوازي, فإذا احتوت الشجرة على n عقدة , كما في الاشجار عدد الوصلات يكون اقل بواحد من عدد العقد الكلي.

الجذور, وصلات التقدم والتراجع:

إذا كان لدى الشجرة جذر, يمكننا أن نقسم اللائحة الحلقية succ عند الجذر في تلك الحالة, يمكننا ذكر وصلات التراجع و التقدم: لديك زوج من العقد u,v,,أول ظهور لأي من (u,v) أو (v,u) في شجرة رحلة أويلر يسمى وصلة التقدم, و الظهور الثاني يسمر وصلة التراجع. هذا يرجع الى فكرة انه في المرة الاولى التي يتم فيها المرور عبر هذه الوصلة يزداد البعد عن الجذر, بينما في المرة الثانية هذا البعد يقل.

إعادة تجذير الشجرة يمكن القيام بها في وقت ثابت هو O(1) من خلال قسم اللائحة الحلقية succ عند الجذر الجديد.

التطبيقات:

كل المسائل التالية يمكن حلها بتعقيد O(Prefix sum(n)) (الوقت المستغرق لحل مسألة المجموع التراكمي ( prefix sum) بالتوازي من أجل لائحة فيها n عنصر):

تصنيف وصلات التراجع والتقدم: قم بترتيب اللائحة على رحلة أويلر و احفظ النتيجة في مصفوفة ثنائية الأبعاد مسماة A ثم (u,v) تكون وصلة التقدم إذا كانت A(u,v) < A(v,u) و وصلة تراجع في حالة العكس.
حدد مستوى كل عقدة: قم ب مجموع البادئات على رحلة أويلر, بحيث كل قيمة وصلة تقدم تساوي 1 و قيمة كل وصلة تراجع تساوي -1. عندها تكون قيمة وصلة التقدم (u,v) هي مستوى v.
عدد العقد في شجرة جزئية معادة التجذير عند v: افترض أن أب v هو u,: حدد وصلة التقدم (u,v) والتراجع (v,u) , ثم احسب عدد وصلات التقدم بين (v,u) و (u,v) مستعملا المجموع التراكمي.
مؤشر البحث بالعمق(depth-first search) اولا لعقدة ما: احسب عدد وصلات التقدم من البداية وحتى (u,v) مع تضمينها.
تحديد تحديد أدنى سلفّ/جد مشترك لعقدتين ما.

أشجار رحلة أويلر:

هينزينغر وكينغ اقترحوا تمثيل شجرة عبر وضع رحلة أويلر الخاصة بها في شجرة بحث ثنائي متوازنة( balanced binary search tree), مرمزة بالمؤشرات في الرحلة. كمثال على ذلك, الشجرة الغير متوازنة في المثال السابق, لديها 7 عقد, سوف تمثل بشجرة بحث ثنائي متوازنة لديها 14 عقدة, واحدة لكل مرة تظهر فيها كل عقدة في الرحلة. يمكننا تمثيل غابة( بيان بدون حلقات) باستعمال مجموعة من أشجار رحلة اويلر- شجرة رحلة أويلر لكل شجرة من الغابة. هذا التمثيل يسمح لنا باجابة سؤال "ما هو جذر العقدة v؟" بسرعة فقط بالانتقال إلى العقدة الأولى في شجرة رحلة أويلر(نظرًا لأن العقد في شجرة رحلة أويلر مرمزة بموقعها في رحلة أويلر، حيث يكون الجذر هي العقدة الأولى والأخيرة في الرحلة). عندما يتم تحديث الغابة الممثلة (مثل ربط شجرتين بشجرة واحدة أو تقسيم شجرة إلى شجرتين)، يمكن تحديث الهيكل المقابل لجولة أويلر في وقت O(log(n)). تتمتع أشجار الوصل/القطع(Link/cut trees) بأداء مشابه. بينما تعتبر أشجار الوصل و القطع جيدة للحفاظ على التجميعات على مسارات الشجرة (مما يجعلها خيارًا جيدًا كهيكل بيانات في خوارزميات تدفق الشبكة)، فإن أشجار رحلة أويلر أفضل في الاحتفاظ بمعلومات التجميع على الأشجار الفرعية.

المراجع:

^[1]

مراجع

^ Tarjan, R.E.; Vishkin, U. (1984). Finding biconnected components and computing tree functions in logarithmic parallel time. Proceedings of FOCS. pp. 12–20. CiteSeerX 10.1.1.419.3088. doi:10.1109/SFCS.1984q5896. ^ Henzinger, M. R.; King, V. (1995). "Randomized dynamic graph algorithms with polylogarithmic time per operation". Proceedings of the twenty-seventh annual ACM symposium on Theory of computing - STOC '95. p. 519. doi:10.1145/225058.225269. ISBN 0-89791-718-9. ^ Euler tour trees - in Lecture Notes in Advanced Data Structures. Prof. Erik Demaine; Scribe: Katherine Lai.

[1] Tarjan, R.E.; Vishkin, U. (1984). Finding biconnected components and computing tree functions in logarithmic parallel time. Proceedings of FOCS. pp. 12–20. CiteSeerX 10.1.1.419.3088. doi:10.1109/SFCS.1984q5896. ^ Henzinger, M. R.; King, V. (1995). "Randomized dynamic graph algorithms with polylogarithmic time per operation". Proceedings of the twenty-seventh annual ACM symposium on Theory of computing - STOC '95. p. 519. doi:10.1145/225058.225269. ISBN 0-89791-718-9. ^ Euler tour trees - in Lecture Notes in Advanced Data Structures. Prof. Erik Demaine; Scribe: Katherine Lai.

[1]