دالة جزئية التشكل
دوال مركبة قابلة للاشتقاق في كل مكان في مجالاتهم
(بالتحويل من دالة جزئية الشكل)
في التحليل العقدي، الدالة جزئية التشكل[1] أو الدالة التحليلية جزئية التشكل[2] أو الدالة تحليلية التشكل الجزئية[3] أو أو الدالة الميرومورفية[4] (بالإنجليزية: Meromorphic function)، تنطلق من مجموعة مفتوحة D ضمن المستوي المركب، هي دالة تحليلية تامة التشكل على جميع عناصر D باستثناء مجموعة معينة من النقاط المعزولة.[5]
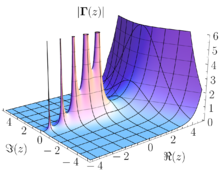
أمثلة
عدلكل الدوال الكسرية،[6] كما يبين المثال التالي:
هي دوال جزئية التشكل في المستوي المركب كله.
انظر أيضًا
عدلمراجع
عدل- ^ "التحليل العقدي"، موسوعة العلوم والتقانات (ط. 1)، دمشق: هيئة الموسوعة العربية، ج. 6، 2015، OCLC:1263678242، QID:Q131028820
- ^ أحمد شفيق الخطيب (2018). معجم المصطلحات العلمية والفنية والهندسية الجديد: إنجليزي - عربي موضح بالرسوم (بالعربية والإنجليزية) (ط. 1). بيروت: مكتبة لبنان ناشرون. ص. 494. ISBN:978-9953-33-197-3. OCLC:1043304467. OL:19871709M. QID:Q12244028.
- ^ أديبة فرح؛ رياض كريم؛ محمد سعيد؛ سليم إدوار (2004). القاموس إنكليزي - عربي: مع الرسم اللاتيني للكلمات الإنكليزية حسب النطق الصوتي، قاموس عام لغوي علمي، يتضمن المصطلحات الطبية والرياضية والفيزيائية والكيميائية والمعلوماتية والهندسية وغيرها (بالعربية والإنجليزية). دار الكتب العلمية. ص. 481. ISBN:978-2-7451-3667-1. OCLC:225745956. OL:20379092M. QID:Q106991021.
- ^ موفق دعبول؛ بشير قابيل؛ مروان البواب؛ خضر الأحمد (2018)، معجم مصطلحات الرياضيات (بالعربية والإنجليزية)، دمشق: مجمع اللغة العربية بدمشق، ص. 442، OCLC:1369254291، QID:Q108593221
- ^ Hazewinkel, Michiel، المحرر (2001) [1994]. "Meromorphic function". Encyclopedia of Mathematics. Springer Science+Business Media B.V. ; Kluwer Academic Publishers. ISBN:978-1-55608-010-4.[وصلة مكسورة]
- ^ Lang، Serge (1999). Complex analysis (ط. 4th). Berlin; New York: شبرينغر. ISBN:978-0-387-98592-3.
 | هذه بذرة مقالة عن التحليل الرياضي بحاجة للتوسيع. فضلًا شارك في تحريرها. |