دالة متباينة
دالة تبقى بها العناصر متباينة
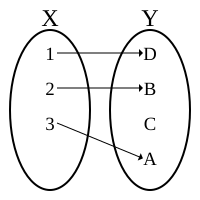
في الرياضيات، الدالة المتباينة (بالإنجليزية: Injective function) هي دالة تبقى بها العناصر متباينة (متفاوتة): فبها لا تقترن العناصر المتباينية من مجالها بنفس العنصر من مجالها المقابل.[1][2][3] بمعنى أن كل عنصر من مجالها المقابل مقترن بعنصر من مجالها واحد على الأكثر.

تعريف
عدللتكن f دالة مجال تعريفها هو مجموعة A. الدالة f هي متباينة إذا وفقط إذا توفر لكل عنصرين a و b من A ما يلي:
- إذا كان (f(a) = f(b، فإن a = b؛ أي أن (f(a) = f(b تعني a = b. وبشكل مكافئ، إذا كان a ≠ b، فإن (f(a) ≠ f(b.
باستعمال رموز الرياضيات، يُحصل على ما يلي:
والتي تكافئ بشكل منطقي ما يلي:
أمثلة
عدل- الدالة المطابقة هي دالة متباينة.
- الدالة f : R → R المعرفة ب f(x) = 2x + 1 هي متباينة.
مراجع
عدل- ^ قالب:Note autre projet
- ^ "Unicode" (PDF). مؤرشف من الأصل (PDF) في 2018-05-23. اطلع عليه بتاريخ 2013-05-11.
- ^ Williams، Peter. "Proving Functions One-to-One". مؤرشف من الأصل في 2000-10-11.
انظر أيضًا
عدلفي كومنز صور وملفات عن Injectivity.