ديناميكا طيران المركبات الفضائية

ديناميكا طيران المركبات الفضائية هي تطبيق الميكانيكا التقليدية لنَمذجة كيفية تحديد القُوى الخارجية المؤثرة على مركبة فضائية لمسار رحلتها. تتكون هذه القُوى بشكل أساسي من ثلاثة أنواع: القوة الدافعة التي توفرها محركات المركبة، وقوة الجاذبية التي تمارسها الأرض والأجرام السماوية الأخرى، والرفع والسحب الديناميكي الهوائي (عند الطيران في الغلاف الجوي للأرض أو أي جسم آخر، مثل المريخ أو الزُهرة).

مسار رحلة هبوط الإنسان على سطح القمر بمركبة أبولو 11، يوليو 1969م.

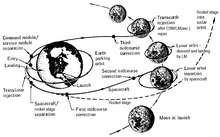
تُستخدم مبادئ ديناميكيات الطيران لنمذجة مسار مركبة أثناء الإطلاق من الأرض؛ والرحلة المدارية للمركبة الفضائية؛ والمناورات لتغيير المدار؛ والرحلة للقمر والكواكب؛ والإطلاق من والهبوط على جرم سماوي - بغلاف جوي أو بدونه؛ والدخول عبر الغلاف الجوي للأرض أو أي جرم سماوي آخر؛ والتحكم بالوضعية. يتم برمجت ديناميكا الطيران عمومًا في أنظمة الملاحة بالقصور الذاتي للمركبة، ويتم مراقبتها على الأرض بواسطة أحد أعضاء فريق مراقبي الطيران المعروف في وكالة ناسا باسم ضابط ديناميكيات الطيران، أو في وكالة الفضاء الأوروبية باسم ملاح المركبة الفضائية.

تعتمد ديناميكيات الطيران على تخصصات الدفع والديناميكا الهوائية والديناميكا الفلكية (ميكانيكا المدارات وميكانيكا السماوات). لا يمكن اختصار الأمر في مجرد التحكم بالوضعية؛ فالمركبات الفضائية الحقيقية لا تحتوي على عجلات قيادة أو مقود مثل الطائرات أو السفن. على عكس الطريقة التي يتم بها تصوير المركبات الفضائية الخيالية، فإن المركبة الفضائية في الواقع لا تميل لتدور في الفضاء الخارجي، حيث يعتمد مسار رحلتها بشكل أساسي على قوى الجاذبية المؤثرة عليها والمناورات المدارية المُطبقة.

المبادئ الأساسية

يُحدد مسار المركبة الفضائية بتطبيق قانون نيوتن الثاني للحركة:$$\mathbf {F} =m\mathbf {a} ,$$ حيث F هو مجموع مُتجهات جميع القوى المؤثرة على المركبة، وm هي كتلتها الحالية، و a هو متجه التسارع، ومعدل التغير اللحظي للسرعة ( v )، والذي بدوره هو معدل التغير اللحظي للإزاحة. عند حل المعادلة ، فإن التسارع يساوي مجموع القوة مقسومًا على الكتلة. يُدمج التسارع مع الزمن للحصول على السرعة، وتُدمج السرعة بدورها للحصول على الموضع (المكان).

تُدار حسابات ديناميكيات الطيران بواسطة أنظمة التوجيه المُحَوسبة على متن المركبة، وتُراقب حالة ديناميكيات الطيران على الأرض أثناء المناورات الآلية بواسطة أحد أعضاء فريق مراقبي الطيران المعروف في مركز رحلات الفضاء البشرية التابع لوكالة ناسا باسم ضابط ديناميكيات الطيران، وفي وكالة الفضاء الأوروبية باسم ملاح المركبة الفضائية.

بالنسبة للطيران الجوي، فإن القوى الرئيسية الثلاث التي تؤثر على المركبة هي القوة الدافعة ، وقوة المقاومة الديناميكية الهوائية ، والجاذبية. القوى الخارجية الأخرى مثل قوة الطرد المركزي وقوة كوريوليس وضغط الإشعاع الشمسي تكون غير مهمة بشكل عام بسبب الوقت القصير نسبيًا للطيران والحجم الصغير للمركبة الفضائية، وقد يتم إهمالها بشكل عام في حسابات الأداء المبسطة.

الدفع

تُقرَّب قوة دفع محرك الصاروخ، في الحالة العامة للتشغيل في الغلاف الجوي، من خلال:

$$F={\dot {m}}\;v_{e}={\dot {m}}\;v_{\text{e-opt}}+A_{e}(p_{e}-p_{\text{amb}})$$حيث أن:

• ${\dot {m}}$ هو تدفق كتلة غاز العادم
• $v_{e}$ هي سرعة العادم الفعالة (يشار إليها أحيانًا باسم c في الأوراق العلمية)
• $v_{\text{e-opt}}$ هي سرعة المركبة النفاثة الفعالة عندما يكون p _amb = p _e
• $A_{e}$ هي مساحة التدفق عند مستوى خروج الفوهة (أو المستوى الذي يغادر فيه النفاثة الفوهة إذا كان التدفق منفصلًا)
• $p_{e}$ هو الضغط الثابت عند مستوى خروج الفوهة
• $p_{\text{amb}}$ هو الضغط المحيط (أو الضغط الجوي)

إن سرعة العادم الفعالة للوقود الصاروخي تتناسب طرديًا مع الدفع النوعي للفراغ وتتأثر بالضغط الجوي: $$v_{e}=g_{0}\left(I_{\text{sp-vac}}-{\frac {A_{e}\,p_{\text{amb}}}{\dot {m}}}\right)$$

حيث أن:

• $I_{\text{sp-vac}}$ هو الدفع نوعي ووحدتها ثانية
• $g_{0}$ هي تسارع الجاذبية على سطح الأرض

يربط الدافع النوعي بين فرق السرعة (دلتا v) وكمية الوقود المستهلك وفقًا لمعادلة تسالكوفسكي الصاروخية: $$\Delta v\ =v_{e}\ln {\frac {m_{0}}{m_{1}}}$$حيث أن:

• $m_{0}$ هي الكتلة الكلية الأولية، بما في ذلك الوقود، بالكيلوجرام.
• $m_{1}$ هي الكتلة الكلية النهائية بالكيلوجرام
• $v_{e}$ هي سرعة العادم الفعالة بوحدة م/ث
• $\Delta v$ هل فرق السرعة( دلتا-v) بوحدة م/ث

متجهات السرعة والموقع والقوة المؤثرة على مركبة فضائية أثناء الإطلاق

متجهات السرعة والقوة المؤثرة على مركبة فضائية أثناء الهبوط والنزول

الرحلة المدارية

لمعلوماتٍ أكثر: ميكانيكا مدارية

تُستخدم ميكانيكا المدار لحساب الرحلة في مدار حول جسم مركزي. بالنسبة للمدارات المرتفعة بما يكفي (عادةً ما 190 كم في حالة الأرض)، يُفترض أن القوة الديناميكية الهوائية يمكن إهمالها للمهام القصيرة الأمد نسبيًا (على الرغم من إمكانية وجود كمية صغيرة من السَحب تؤدي إلى تدهور الطاقة المدارية على مدى فترات زمنية أطول). وعندما تكون كتلة الجسم المركزي أكبر بكثير من المركبة الفضائية، وتكون الأجسام الأخرى بعيدة بما يكفي، يُمكن التعامل مع حل المسارات المدارية كمشكلة جسمين.

تتميز المدارات الإهليلجية بثلاثة عناصر. المحور شبه الرئيسي a وهو متوسط نصف القطر عند القَبَا (الأوج والحضيض) : $$a={\frac {r_{a}+r_{p}}{2}}$$

يمكن بعد ذلك حساب الانحراف المداري e للقطع الناقص، مع معرفة الزوايا: $$e={\frac {r_{a}}{a}}-1$$

تعتمد الفترة الزمنية للمدار الكامل فقط على المحور شبه الرئيسي، وهي مستقلة عن الانحراف: $$T=2\pi {\sqrt {\frac {a^{3}}{\mu }}}$$ حيث أن $\mu$ هو معامل الجاذبية القياسي للجسم المركزي.

العناصر المدارية الزاوية للمركبة الفضائية التي تدور حول جسم مركزي، والتي تحدد اتجاه المدار بالنسبة إلي مستوى مرجعي.

أنواع المدارات

دائري

بالنسبة للمدار الدائري، r _a = r _p = a ، والانحراف يساوي 0. السرعة الدائرية عند نصف قطر معين هي: $$v_{c}={\sqrt {\frac {\mu }{r}}}$$

إهْلِيلَجي

بالنسبة للمدار الإهليلجي، e أكبر من 0 ولكن أقل من 1. سرعة الحضيض هي: $$v_{p}={\sqrt {\frac {\mu (1+e)}{a(1-e)}}}$$ وسرعة الأوج هي: $$v_{a}={\sqrt {\frac {\mu (1-e)}{a(1+e)}}}\,$$