تعمية قيصر
تعمية قيصر، تسمى أيضا تشفير الإزاحة، هي طريقة من طرق التعمية التقليدية (بالإنجليزية: Classical Cryptography) تستعمل لتعمية النصوص، شاع استخدام هذه الطريقة قديمًا ويُعتقد أن يوليوس قيصر كان أول من استخدم هذه الوسيلة بين 58 ق.م حتى 51 ق.م. تتميز هذه الشفرة بسهولة تطبيقها لذلك تعتمد غالبا كمدخل للتعرف على علم التعمية التقليدي غير أنها ليست أقدم طريقة تعمية مسجلة تاريخيا، إذ تعود أول محاولة تاريخية مسجلة لممارسة فن التعمية إلى العام 1900 قبل الميلاد.[1] فكرة الطريقة مشابهة لحد ما لتعمية أتبش ولطرق أخرى كانت منتشرة قديما، بحيث أنها تعتمد على مقابلة حروف الأبجدية بنسخة محوَّرة من نفس الحروف وذلك باعتماد تحوير بسيط غالبا ما يكون سريا ومتفق عليه. ويقوم مبدأ شفرة قيصر أو شفرة الإزاحة على مقابلة حروف الأبجدية بنسخة من نفس الأحرف تمت إزاحتها بموضع ثلاثة أحرف، فمثلا تشفير حرف «أ» يكون هو حرف «ث» وتشفير الكلمة «مرحبا» يكون بذلك هو «وشذجث». وكما جاء على لسان المؤرخ الروماني سويتونيوس في كتابه القياصرة الاثنى عشر، فإن أغسطس قيصر، و هو ابن أخ يوليوس قيصر، استخدم هو الآخر نفس المبدأ للتشفير، غير أنه كان يعتمد على إزاحة بمقدار موضع واحد فقط، مع تعمية آخر حرف في الأبجدية بتكرار أول حرف من الأبجدية مرتين.
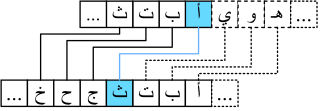
لا يمكن اعتبار تعمية قيصر خوارزمية تعمية حقيقية حسب المعايير الحالية لأنها لا تحترم مبادئ كيرشوف وخصوصا مبدأ الإعتماد على سرية المفتاح وليس على سرية الخوارزمية.[2] بذلك تكون تعمية قيصر مثل سائر الطرق القديمة غير آمن البتة إذ أنه انطلاقا من النص المعمى يمكن استنباط النص الأصلي، وذلك لأن طبيعة توزيع الحروف في النص لا تتغير وبالتالي حسب طبيعة التوزيع الأصلي للغة الأصل يمكن استنباط النص الأصلي، هذا النوع من الهجمات يسمى: هجوم النص المعمى المعروف. رغم انعدام الحماية عند استخدام تعمية قيصر إلا أنها تجد استخدامات لها (في صيغتها العامة) في بعض الحالات التي لا تستدعي حماية بقد ما تستدعي إخفاء لحظي للنص كخوارزمية روت 13 التي تستخدم في العديد من المواضع كالمجلات وبعض الأجهزة الإلكترونية.
اصطلاحات
عدلقبل البدء بتوصيف تعمية قيصر لا بد من توضيح بعض الاصطلاحات الرئيسة:
- النص الواضح (يسمى أيضا النص المجرد) وهو النص الأصل المراد تعميته، سيُرمز له بالحرف وهو مركب من مجموعة من الحروف، كل حرف ينتمي لمجموعة تُسمى الأبجدية، نرمز لهذه الأبجدية بالحرف ، و نقول أن هو نص مكون من حرف. مثلا: كلمة «مرحبا» هي نص واضح ينتمي ل مجموعة النصوص المكونة من خمسة حروف، بحيث مجموعة حروف الأبجدية العربية.
- النص المعمى وهو نتيجة تطبيق خوارزمية التعمية على النص الواضح، سيُرمز له بالحرف . في حالة تعمية قيصر أو تعمية الإزاحة إذا كان فإن أيضا، أي بعبارة أخرى و لهما الطول نفسه.
- دالة التعمية أو خوارزمية التعمية، نرمز لها ب ، و هي الخوارزمية التي تربط النص الواضح بالنص المعمى كما يلي: بحيث هو مفتاح التعمية. في حالة تعمية قيصر فلا حاجة لمفتاح لأن التعمية ثابتة وتعتمد فقط على خوارزمية التعمية، لذلك يمكننا صياغة هذه العلاقة في هذه الحالة ب .
- دالة فك التعمية أو خوارزمية فك التشفير، سنرمز لها ب ، وهي تَعْكُس عمل خوارزمية التعمية ، أي أنها تربط النص المعمى بالنص الواضح كما يلي: . في حالة تعمية قيصر فلا حاجة لمفتاح لذلك يمكننا صياغة هذه العلاقة في هذه الحالة ب .
عملية التشفير وفك التشفير
عدلتعمية قيصر
عدللا تعتمد خوارزمية تعمية قيصر على مفتاح سري لكنها تعتمد على سرية الخوارزمية. تعوض الخوارزمية ببساطة كل حرف بحرف يليه في الترتيب الأبجدي بعدد محدد من الحروف، بعبارة أخرى، لنفترض أن مجموعة الحروف الأبجدية مرقمة ترتيبيا وفق الجدول الآتي. ( سنستخدم للدلالة على مجموعة الحروف ونظيرتها من مجموعة الأعداد بشكل متماثل في ما يلي):
| الحرف الأبجدي | أ | ب | ت | ث | ج | ح | خ | د | ذ | ر | ز | س | ش | ص | ض | ط | ظ | ع | غ | ف | ق | ك | ل | م | ن | ه | و | ي |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| الرقم الترتيبي | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 |
عملية تعمية قيصر هي خوارزمية معرفة كالآتي:
مثال
عدللتعمية الكلمة «مرحبا» يُعمَّى كل حرف على حدة باستخدام الخوارزمية . لتعمية هذه الحروف يجب مقابلة كل حرف بالرقم المقابل له، مثلًا حرف «م» يقابله العدد 23 في الجدول أعلاه، فيكون بذلك تشفير حرف «م» هو الحرف المقابل ل أي هو الحرف «و».
يُطبق المبدأ نفسه لتعمية سائر الحروف فيكون على النص المعمى «وشذجث».
يمكن إنجاز النعمية يدويًا أو آليًا باعتماد هذه الخوارزمية التي تعتمد على الحسابيات المعيارية.
فك التعمية
عدليمكن تصنيف تعمية قيصر ضمن خوارزميات تعمية بالمفتاح المتناظر، وبذلك سنعتمد فقط على عكس خوارزمية التعمية لصياغة خوارزمية فك التعمية التي سيُرمز لها ب . ويمكن تعريف كالآتي:
بعبارة أخرى فإن تحول كل حرف إلى الحرف الثالث قبله في الترتيب الأبجدي.
تعميم تعمية قيصر: التعمية بالإزاحة
عدللا تعتمد تعمية قيصر في الأصل على أي مفتاح سري بل على سرية الخوارزمية. يمكن تعميم تعمية قيصر وذلك بإدخال متغير يمثل المفتاح السري الذي يمثل قيمة الإزاحة اللتي ينبغي تطبيقها على حروف الأبجدية. من الواضح أن هذه القيمة السرية لا يجب أن تكون منعدمة (لأنه في هذه الحالة لن يكون هناك أي تعمية)، كما أنه لن يكون هناك معنى لاختيار قيمة أكبر من أو تساوي حجم الأبجدية (مثلا باختيار المفتاح 28، وهو عدد حروف الأبجدية العربية، لن يكون هناك أي تعمية). وبالتالي نعرف المفتاح بحيث تمثل عدد عناصر الحروف الأبجدية. في حالتنا هذه والتي نهتم من خلالها بأبجدية الأحرف العربية، فإن المفتاح ينبغي أن ينتمي للمجموعة .
يعاد تعريف خوارزمية التعمية في هذه الحالة العامة كالآتي:
ويعاد تعريف خوارزمية فك التعمية المقابلة لها كما يلي:
يمكننا التأكد من صحة الخوارزمية (بالإنجليزية: proof of correctness) ببساطة كما يلي:
مثال
عدللتعمية الرسالة التالية «ويكيبيديا» باستخدام مفتاح تعمية . تُطبَّق الخوارزمية باستخدام المفتاح المختار على كل حرف على حدة:
بالتالي، يكون النص المعمى هو «سشخشضشقشص».
نص برمجي
عدلفيما يلي نص برمجي بلغة بايثون يوضح عمليتي التعميةوفك التعمية باعتماد مفتاح إزاحة معين. تُستعمل أبجدية اللغة العربية المعرفة حسب الترميز الموحد كما يلي (تضم 29 حرف باعتبار التاء المروبوطة كحرف مستقل):
alphabet = [*range(0x0627, 0x063B), *range(0x0641, 0x0649), 0x064A] # أبجدية عربية
النص البرمجي للتعمية
عدلdef encrypt(key, message, alphabet):
ciphertext = []
for letter in message:
try:
i = alphabet.index(ord(letter))
except:
ciphertext.append(letter)
else:
ciphertext.append(chr(alphabet[(i + key) % len(alphabet)]))
return "".join(ciphertext)
النص البرمجي لفك التعمية
عدلdef decrypt(key, ciphertext, alphabet):
plaintext = []
for letter in ciphertext:
try:
i = alphabet.index(ord(letter))
except:
plaintext.append(letter)
else:
plaintext.append(chr(alphabet[(i - key) % len(alphabet)]))
return "".join(plaintext)
مثال تطبيقي
عدلالنص الواضح: مرحبا من ويكيبيديا الموسوعة الحرة
النص المعمى: كدثيو كل نهفهيهحهو وقكنرنطا وقثدا
تحليل أمن شفرة قيصر
عدلكما هو معلوم، فإن شفرة قيصر الأصلية لا تعتمد على مفهوم المفتاح لتشفير النصوص بل تعتمد على سرية الخوارزمية، وهذا يخرق مبادئ كيرشوف كما تمت الإشارة سابقا في هذا المقال. لذلك سنعتمد على شفرة الإزاحة (شفرة قيصر العامة) والتي تعتمد على مفهوم المفتاح والتي تم تناولها في الفقرة السابقة للقيام بتحليل أمن الشفرة.
شفرة قيصر ليست آمنة الدلالة
عدلبالعودة إلى المثال الأول من الفقرة السابقة، يمكنك ملاحظة وجود تطابق نمطي بين النص الواضح والنص المشفر. بعبارة أخرى، يمكنك ملاحظة أن حرف الياء في النص «ويكيبيديا» دائما ما يتم تشفيره باستخدام حرف الشين في النص المشفر «سشخشضشقشص». وبالتالي يمكن لأي خصم التفريق بين شفرتين مختلفتين فقط بتحليل النصوص المشفرة. لتوضيح هذا الأمر سنفترض السيناريو التالي: نفترض أن هناك خصم متنصت على محادثة مشفرة بين طرفين، قام خلالها برصد الشفرة «نبن». نفترض أن المتنصت يعلم مسبقا أن هذه الشفرة هي جواب لسؤال معلوم يقبل فقط إجابتين هما: «فجر» أو «ليل». واضح من تحليل الشفرة فقط، ودون الحاجة لكسرها أو محاولة معرفة المفتاح، أن النص الواضح الموافق للنص المشفر «نبن» هو «ليل» وليس «فجر»، لأن هناك تطابق في أنماط الكلمتين «نبن» و«ليل» (كلاهما يبدءان بحرف وينتهيان بنفس الحرف) . نقول في هذه الحالة إن شفرة قيصر ليست آمنة دلاليا (بالإنجليزية: semantically secure).
طرق كسر شفرة قيصر
عدلنتناول في هذه الفقرة بعض طرق كسر شفرة قيصر بشكل عام، أي أننا سنستخدم العبارتين شفرة قيصر و شفر الإزاحة للدلالة على الحالة العامة حيث يكون هناك مفتاح سري .
هجوم الإكراه الأعمى
عدلقد يسمى أيضا هجوم القوة العمياء، (بالإنجليزية: Brute-force attack)، وهو ببساطة هجوم يقتضي تجريب كل المفاتيح الممكنة إلى غاية إيجاد المفتاح الصحيح. نُذَكِّر أن حقل المفاتيح الممكنة صغير جدا ، و بالتالي تجريب كل هذه المفاتيح لن يتطلب مجهود ووقت كبيرين قبل العثور على المفتاح المناسب. يمكن القيام بهجوم الإكراه الأغمى في حالتنا هذه سواء يدويا أو آليا.
هجوم التحليل الإحصائي
عدلهجوم التحليل الإحصائي أو تحليل التكرار (بالإنجليزية: frequency analysis)، هو طريقة من أبرز طرق تحليل الشفرات التقليدية وهو من اختراع وتطوير العرب.[1] ولعل هذه كانت أول محاولة تاريخية لتطوير علم رياضي يهتم بكسر وتحليل الشفرات، وقد كان يسميه العرب حينها علم استخراج المعمَى.[3] يقوم مبدأ هذا النوع من الهجمات على استخدام التحليل الإحصائي للغة الشفرة وللشفرة ذاتها ومحاولة مطابقة تردد حروف الشفرة مع تردد حروف اللغة الأصلي، وبذلك يتمكن المحلل من التوصل إلى تقابل بين أبجدية النص الواضح وأبجدية النص المشفر. يستطيع هذا النوع من الهجمات كسر كل شفرات الإبدال الأحادي بدون استثناء، والتي من ضمنها شفرة قيصر و شفرات الإزاحة وشفرات أخرى عديدة. مثلا، باعتبار اللغة العربية، نعلم انطلاقا من تحليل التكرار أن حرف الألف هو أكثر الأحرف تواترا في اللغة، يليه حرف اللام. انطلاقا من هذه المعلومة يمكننا موافقة حرف الألف بالحرف الأكثر تواترا في النص المشفر (مثلا ليكن هو حرف الصاد)، و هكذا نستطيع كشف مفتاح الإزاحة المعتمد في تشفير الإزاحة والذي يكون في هذه الحالة هو 13.
بصيغة أخرى مماثلة، يمكن أيضا الاعتماد على مؤشر التطابق (بالإنجليزية: index of coincidence)، و هو مؤشر مبني على التحليل الإحصائي للغة يتم استخدامه لتحليل وكسر عدد من الشفرات التقليدية. لكن يجب التنويه إلى أنه للقيام بهجوم تحليل التكرار يجب أن يكون بحوزة المهاجم كم كافي من النصوص المشفرة.
مصادر
عدل- ^ تعدى إلى الأعلى ل: ا ب Kahn David (1996). The Codebreakers: The Comprehensive History of Secret Communication from Ancient Times to the Internet. Simon and Schuster.
- ^ Kerckhoffs Auguste (1883). La cryptographie militaire. Journal des sciences militaires.
- ^ د. محمد مراياتى, يحى مير علم, محمد حسان الطيان (1988). علم التعمية واستخراج المعمى عند العرب. مجمع اللغة العربية بدمشق.
{{استشهاد بكتاب}}: صيانة الاستشهاد: أسماء متعددة: قائمة المؤلفين (link)
