في الهندسة الرياضية، مبرهنة أو نظرية منصف زاوية هي مبرهنة في المثلث تعطي العلاقة بين طول الضلع المقابل لأي زاوية إلى طول الضلعين الباقيين.[1] وتنص على أنه في المثلث ABC، إذا كان AD منصف للزاوية A وكانت D نقطة تقاطع AD مع BC فإن:
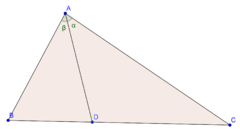 AD منصف للزاوية A
AD منصف للزاوية A

مبرهنة مُنصّف الزّاوية هي حالة خاصّة من القانون النّاص على أنه: في المثلث ABC، إذا كان AD يقطع BC في D ويقسم الزاوية A إلى و فإن:
وعندما تصبح مبرهنة منصف الزاوية.
المثلث ABC
باستخدام قوانين مساحة المثلث:
1- مساحة المثلث ADC
2- مساحة المثلث ADB
بقسمة 2 على 1 نصل إلى:
و إذا كان AD منصف الزاوية A ستحقق المبرهنة و ذلك لأن .
AD منصف للزاوية A
باستخدام قانون الجيوب:
في المثلث ADC:
في المثلث ADB:
و (Sin x = Sin (180-x.
و إذا كانت سنصل إلى مبرهنة منصف الزاوية.
المثلث ABC
برهان هندسي، باستخدام تشابه المثلثات:
ِAD منصف الزاوية A، نسقط عمود من B على AD يقطعه في F، ونسقط عمود من C على امتداد AD يقطعه في E.
المثلث AEC يشابه المثلث AFB
( لأن E و F قائمتان و لأن AD منصف A)
المثلث DEC يشابه المثلث DFB
( لأن E و F قائمتان و للتقابل بالرأس)
وهو المطلوب إثباته .

