عدد غير كسري
في الرياضيات، الأعداد غير الكسرية أو الأعداد غير النسبية أو الأعداد غير القياسية أو الأعداد غير المُنطَّقة[1] أو الأعداد غير الجذرية أو الأعداد الصماء[1] أو الجذور الصماء (بالإنجليزية: Irrational number) هي الأعداد الحقيقية التي لا يمكن كتابتها على صورة كسر اعتيادي (أي كسر بسطه ومقامه عددان صحيحان ومقامه يختلف عن الصفر).
| صنف فرعي من | |
|---|---|
| جزء من | |
| النقيض |
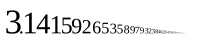
وبتعبير آخر، الأعداد غير النسبية لا يمكن أن تُمثل على شكل كسر بسيط. فالأعداد غير النسبية هي الأعداد الحقيقية التي ليس لها تمثيل عشري منته أو متكرر. ونتيجة على برهان كانتور على كون الأعداد الحقيقية غير قابلة للعد (وأن الأعداد النسبية قابلة للعد)، فإن الأعداد الحقيقية كلها تقريبا غير نسبية.
قد تكون الثوابت الرياضية وعدد أويلر والجذر التربيعي ل 2, والنسبة الذهبية φ من أشهر الأعداد غير الكسرية.
التاريخ
عدلانظر إلى الرياضيات الهندية.
الإغريق
عدلالهند
عدلالعصور الوسطى
عدلفي العصور الوسطى، طور علمَ الجبر علماء الرياضيات المسلمون. مكن ذلك من التطرق إلى الأعداد غير النسبية باعتبارها كائنات جبرية. وقد جمع علماء رياضيات الشرق الأوسط بين مفهومي العدد والمقدار، في فكرة واحدة أكثر عمومية تتمثل في الأعداد الحقيقية، كما انتقدوا مفهوم النسبة الذي قدمه أقليدس.
درس وصنف عالمُ الرياضيات الفارسي المهاني (توفي في عام بين عامي 874 و884) خلال تعليقه على الجزء العاشر لكتاب العناصر، الأعداد غير الكسرية التربيعية والأعداد غير الكسرية التكعيبية.
كان عالم الرياضيات المصري أبو كامل شجاع بن أسلم هو أول من قبِل بالأعداد غير الجذرية حلولا لمعادلات تربيعية أو معاملات لهن، عادة على شكل جذور تربيعية أو تكعيبية أو رباعية. عمل في المجال أيضا، عالم الرياضيات العراقي الهاشمي وعالم الرياضيات أبو جعفر الخازن.
قد يكون قد قبِل علماء الرياضيات الأوروبيين العديد من هذه المفاهيم بعد الترجمة إلى اللاتينية لعمل عالم الرياضيات والإرث المغربي أبي بكر الحصار، والذي عاش خلال القرن الثاني عشر في مدينة فاس. هو أول من أشار إلى استعمال الكسور عازلا البسط عن المقام بخط أفقي. ظهر هذا الرمز بُعيد ذلك في عمل ليوناردو فيبوناتشي في القرن الثاني عشر.
حاليا
عدلفي القرن السابع عشر، صارت الأعداد التخيلية أداة قوية بين يدي أبراهام دي موافر وخصوصا ليونهارد أويلر.
لقيت الكسور المستمرة، لأنها شديدة الارتباط بالأعداد غير النسبية (عمل بييترو كاتالدي على ذلك في حوالي عام 1613)، اهتماما كبيرا من طرف ليونهارد أويلر، ومع بداية القرن التاسع عشر، جُلبت إلى شهرة كبيرة بفضل كتابات جوزيف لوي لاغرانج. كما أضاف دركليه ومساهمون آخرون إضافات كثيرة إلى هذا المجال.
برهن يوهان هاينغيش لامبرت في عام 1761، أن العدد π لا يمكن أن يكون نسبيا، وأن العدد en هو أيضا غير نسبي ما دام n يختلف عن الصفر.
أدريان ماري ليجاندر، (في عام 1794)، بعدما أن قدم دالة بيسل-كليفورد، أعطى برهانا يبين أن π2 عدد غير نسبي مما يدل مباشرة بأن π هو أيضا عدد غير نسبي. ولقد برهن على وجود الأعداد المتسامية لأول مرة من طرف جوزيف ليوفيل (1844، 1851). فيما بعد، برهن جورج كانتور (1873) على وجودهم بطريقة أخرى، مبرهنا بذلك وجود أعداد متسامية في أي مجال من الأعداد الحقيقية. في عام 1873، برهن تشارلز هيرمت على أن e عدد متسام. ثم برهن فيردينوند فون ليندمان في عام 1882، اعتمادا على نتائج هيرميت، على أن π هو أيضا عدد متسام. ولقد بُسط برهانه عام 1885 من طرف كارل ويرستراس، وبسط بشكل أكبر في عام 1893 من طرف ديفيد هيلبرت. وفي نهاية المطاف، بُسط هذا البرهان إلى مستوى ابتدائي من طرف أدولف هورفيتز وبول غوردان.
أمثلة للبراهين
عدلالجذور التربيعية
عدلالجذر التربيعي ل 2 هو أول عدد عُرف عنه بأنه عدد غير نسبي. العدد الذهبي هو ثاني عدد اشتهر بكونه عددا غير كسري. الجذر التربيعي لأي عدد صحيح موجب ليس بمربع كامل هو عدد غير نسبي.
الأعداد غير الكسرية المتسامية والأعداد غير الكسرية الجبرية
عدلتقريبا جميع الأعداد غير الكسرية هي أعداد متسامية وجميع الأعداد الحقيقية المتسامية هي أعداد غير كسرية (هناك أيضا أعداد متسامية عقدية). e r و π r أعداد غير كسرية إذا كان r ≠ 0، على سبيل المثال، eπ هو عدد غير كسري.
مسائل مفتوحة
عدللا يُعرف هل العددان π + e و π − e هما نسبيان أم لا. وبشكل أكثر عموما، لا يُعرف هل يوجد عددان صحيحان m و n حيث يعلم العدد mπ + ne هل هو كسري أم لا. بالإضافة إلى ذلك، لا يُعرف هل المجموعة {π, e} مستقلة جبريا أم لا على مجموعة الأعداد الكسرية Q.
لا يُعرف هل πe و π/e و 2e و ee و eee و πe و π و الجذر التربيعي ل 2 ولوغاريتم طبيعي π و ثابتة كاتالان وثابتة أويلر-ماسكيروني γ أعداد كسرية أم غير كسرية.
مجموعة الأعداد غير النسبية
عدلهي الجذور التي تكون مربعاتها ليست كاملة مثل 7√ و 5√
انظر أيضًا
عدلهوامش وملاحظات
عدل- ^ ا ب موفق دعبول؛ بشير قابيل؛ مروان البواب؛ خضر الأحمد (2018)، معجم مصطلحات الرياضيات (بالعربية والإنجليزية)، دمشق: مجمع اللغة العربية بدمشق، ص. 364، OCLC:1369254291، QID:Q108593221


